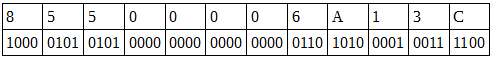Es exactamente la misma idea que la letra del DNI. En ese caso, para calcular el checksum de un DNI la fórmula la marca el Ministerio del Interior y se basa en dividir el nº entre 23 (un valor arbitrario). El resto de esa división se compara con los valores de la siguiente tabla:
Ver el archivo adjunto 20049
Así, un mismo nº de DNI no puede tener dos letras diferentes y le corresponderá una y solo una letra que permitirá verificar que ese número es correcto.
Pues lo mismo en Mazda. Algún iluminado creó una fórmula que comprueba que los dígitos que se introduzcan + el nº de checksum garanticen la estabilidad de la cadena, asegurando que si se introduce erróneamente ésta o el propio checksum, de un error a la hora de guardar la información. La diferencia entre la fórmula de Mazda y la del M.I. es que esta última es pública y la de Mazda es privada, por lo que es complicado saber como calcularla. (No estoy muy al día con este tema y no se si alguien ya ha dado con ello).
Por otra parte, la cadena en hexadecimal activa o desactiva grupos de bits. Por ejemplo, para el caso de la cadena:
Ver el archivo adjunto 20050
Cada dígito representa un nº que puede ir del 0 al 15 (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F) y éste a su vez se descompone en 4 bits, que en aritmética binaria pueden representar 16 valores (0 al 15)
Cada vez que se cambia el valor de un bit, para activarlo o desactivarlo, cambia el nº asociado.
Os pongo un ejemplo:
el valor de más a la derecha es el nº 0xC (12 en decimal) y este corresponde a la cadena de bits "1100". Esto es así porque el valor decimal de cada bit se calcula en potencias de dos, por tanto 2^3 * 1 + 2^2 * 1 + 2^*1 * 0 + 2^0 * 0 = 8 + 4 + 0 + 0 = 12.
Si cambiamos el bit de más a la derecha por un 1 tendríamos entonces el siguiente valor: 1101, en lugar de 1100. Al convertir este nº en hexadecimal nos quedaría de la siguiente manera:
2^3 * 1 + 2^2 * 1 + 2^1 * 0 + 2^0 * 1 = 8 + 4 + 0 + 1 = 13 (0xD)
Por tanto la cadena pasaría a ser 8550 0006 A13
D, en lugar de 8550 0006 A13
C.
Dicho todo este rollazo, la idea es que cambiando los 0 por 1 y viceversa, es posible activar opciones de menú o desactivarlas. ¿Como es posible saber cuales hay que activar y desactivar? La mala noticia es que no se puede saber. La buena es que con el prueba y error y conociendo la fórmula de cálculo del checksum, si sería posible ver que combinaciones hay. Pero se necesita mucha paciencia y tiempo y aún así te arriesgas a dejar frito algo por desconocimiento.
Perdonad si he cometido algún error, pero estoy escribiendo de memoria recordando mis tiempos de estudiante.